Coin rotation paradox
The coin rotation paradox is the counter-intuitive observation that, when one coin is rolled around the rim of another coin of equal size, the moving coin completes two full rotations after going all the way around the stationary coin.[1]
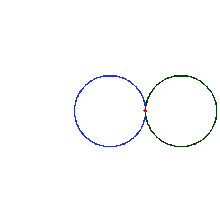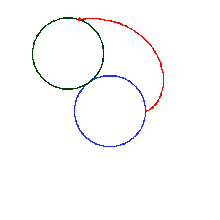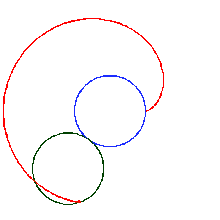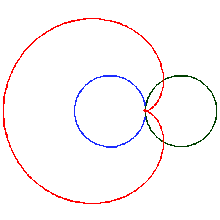
Description
Start with two identical coins touching each other on a table, with their "head" sides displayed and parallel. Keeping coin A stationary, rotate coin B around A, keeping a point of contact with no slippage. As coin B reaches the opposite side, the two heads will again be parallel; B has made one revolution. Continuing to move B brings it back to the starting position and completes a second revolution. Paradoxically, coin B has rolled a distance equal to twice its circumference.
As coin B rotates, each point on its perimeter describes (moves through) a cardioid curve.
Comparison
The rolling coin participates in two separate motions like the moon relative to the earth (except that the moon completes only one rotation about every 28 days). The moon rotates once while revolving around an elliptical pathway relative to true north while the moving coin rotates twice as it revolves around the center of the other (still) coin.

Analysis and Solution
From start to end the center of the moving coin travels a circular path. The edge of the stationary coin and said path form two concentric circles. The radius of the path is twice either coin's radius. Hence, the circumference of the path is twice either coin's circumference. To go all the way around the stationary coin, the center of the moving coin must travel twice the coin's circumference. How much the moving coin rotates around its own center en route, if any, or in what direction – clockwise, counterclockwise, or some of both – has no effect on the length of the path. That the coin rotates twice as described above and focusing on the edge of the moving coin as it touches the stationary coin are distractions.
Unequal radii and other shapes

A coin of radius r rolling around one of radius R makes R/r + 1 rotations.[2] That is because the center of the rolling coin travels a circular path with a radius and circumference of (R + r)/r = R/r + 1 times its own radius and circumference.
In the limiting case when R = 0, the coin with radius r makes 0/r + 1 = 1 simple rotation around its bottom point. In the example in the figure, R = 3r. In figure 1, if R is straightened out, the number of rotations (number of times the arrow points upward) is R/r = 3. In figure 2, as R has been restored into a circle, the coin with radius r makes an extra rotation, giving R/r + 1 = 4.
The shape around which the coin is rolled need not be a circle: one extra rotation is added to the ratio of their perimeters when it is any simple polygon or closed curve which does not intersect itself. If the shape is complex, the number of rotations added (or subtracted, if the coin rolls inside the curve) is the absolute value of its winding number.