Yang–Baxter equation

In physics, the Yang–Baxter equation (or star-triangle relation) is a consistency equation which was first introduced in the field of statistical mechanics. It depends on the idea that in some scattering situations, particles may preserve their momentum while changing their quantum internal states. It states that a matrix $R$ , acting on two out of three objects, satisfies

(R\otimes \mathbf {1} )(\mathbf {1} \otimes R)(R\otimes \mathbf {1} )=(\mathbf {1} \otimes R)(R\otimes \mathbf {1} )(\mathbf {1} \otimes R)

In one dimensional quantum systems, $R$ is the scattering matrix and if it satisfies the Yang–Baxter equation then the system is integrable. The Yang–Baxter equation also shows up when discussing knot theory and the braid groups where $R$ corresponds to swapping two strands. Since one can swap three strands two different ways, the Yang–Baxter equation enforces that both paths are the same.

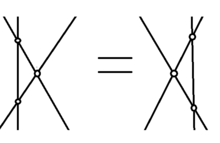
Illustration of Yang Baxter Equation

It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971.

Parameter-dependent Yang–Baxter equation

Let $A$ be a unital associative algebra. The parameter-dependent Yang–Baxter equation is an equation for $R(u)$ , a parameter-dependent invertible element of the tensor product $A\otimes A$ (here, $u$ is the parameter, which usually ranges over real numbers ℝ in the case of an additive parameter, or over positive real numbers ℝ⁺ in the case of a multiplicative parameter).

Let $R_{ij}(w)=\phi _{ij}(R(w))$ for $i,j=1,...,3$ , with algebra homomorphisms $\phi _{ij}:A\otimes A\to A\otimes A\otimes A$ determined by

\phi _{12}(a\otimes b)=a\otimes b\otimes 1,

\phi _{13}(a\otimes b)=a\otimes 1\otimes b,

\phi _{23}(a\otimes b)=1\otimes a\otimes b.

The Yang–Baxter equation for additive parameters is

R_{12}(u)\ R_{13}(u+v)\ R_{23}(v)=R_{23}(v)\ R_{13}(u+v)\ R_{12}(u),

for all values of $u$ and $v$ . For a multiplicative parameter, the Yang–Baxter equation is

R_{12}(u)\ R_{13}(uv)\ R_{23}(v)=R_{23}(v)\ R_{13}(uv)\ R_{12}(u),

for all values of $u$ and $v$ .

In some cases, the determinant of $R(u)$ can vanish at specific values of the spectral parameter $u=u_{0}$ . Some $R$ matrices turn into a one dimensional projector at $u=u_{0}$ . In this case a quantum determinant can be defined .

Parameter-independent Yang–Baxter equation

Let $A$ be a unital associative algebra. The parameter-independent Yang–Baxter equation is an equation for $R$ , an invertible element of the tensor product $A\otimes A$ . The Yang–Baxter equation is

R_{12}\ R_{13}\ R_{23}=R_{23}\ R_{13}\ R_{12},

where $R_{12}=\phi _{12}(R)$ , $R_{13}=\phi _{13}(R)$ , and $R_{23}=\phi _{23}(R)$ .

Let $V$ be a module of $A$ . Let $T:V\otimes V\to V\otimes V$ be the linear map satisfying $T(x\otimes y)=y\otimes x$ for all $x,y\in V$ . Then a representation of the braid group, $B_{n}$ , can be constructed on $V^{{\otimes n}}$ by $\sigma _{i}=1^{\otimes i-1}\otimes {\check {R}}\otimes 1^{\otimes n-i-1}$ for $i=1,\dots ,n-1$ , where ${\check {R}}=T\circ R$ on $V\otimes V$ . This representation can be used to determine quasi-invariants of braids, knots and links.

References

H.-D. Doebner, J.-D. Hennig, eds, Quantum groups, Proceedings of the 8th International Workshop on Mathematical Physics, Arnold Sommerfeld Institute, Clausthal, FRG, 1989, Springer-Verlag Berlin, ISBN 3-540-53503-9.
Vyjayanthi Chari and Andrew Pressley, A Guide to Quantum Groups, (1994), Cambridge University Press, Cambridge ISBN 0-521-55884-0.
Jacques H.H. Perk and Helen Au-Yang, "Yang–Baxter Equations", (2006), arXiv:math-ph/0606053.

External links

Hazewinkel, Michiel, ed. (2001) [1994], "Yang-Baxter equation", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

Yang–Baxter equation

Parameter-dependent Yang–Baxter equation

Parameter-independent Yang–Baxter equation

See also

References

External links