List of aperiodic sets of tiles

Click "show" for description.
A periodic tiling with a fundamental unit (triangle) and a primitive cell (hexagon) highlighted. A tiling of the entire plane can be generated by fitting copies of these triangular patches together. In order to do this, the basic triangle needs to be rotated 180 degrees in order to fit it edge-to-edge to a neighboring triangle. Thus a triangular tiling of fundamental units will be generated that is mutually locally derivable from the tiling by the colored tiles. The other figure drawn onto the tiling, the white hexagon, represents a primitive cell of the tiling. Copies of the corresponding patch of coloured tiles can be translated to form an infinite tiling of the plane. It is not necessary to rotate this patch in order to achieve this.

In geometry, a tiling is a partition of the plane (or any other geometric setting) into closed sets (called tiles), without gaps or overlaps (other than the boundaries of the tiles).[1] A tiling is considered periodic if there exist translations in two independent directions which map the tiling onto itself. Such a tiling is composed of a single fundamental unit or primitive cell which repeats endlessly and regularly in two independent directions.[2] An example of such a tiling is shown in the adjacent diagram (see the image description for more information). A tiling that cannot be constructed from a single primitive cell is called nonperiodic. If a given set of tiles allows only nonperiodic tilings, then this set of tiles is called aperiodic.[3] The tilings obtained from an aperiodic set of tiles are often called aperiodic tilings, though strictly speaking it is the tiles themselves that are aperiodic. (The tiling itself is said to be "nonperiodic".)

The first table explains the abbreviations used in the second table. The second table contains all known aperiodic sets of tiles and gives some additional basic information about each set. This list of tiles is still incomplete.

Explanations

AbbreviationMeaningExplanation
E2Euclidean planenormal flat plane
H2hyperbolic planeplane, where the parallel postulate does not hold
E3Euclidean 3 spacespace defined by three perpendicular coordinate axes
MLDMutually locally derivabletwo tilings are said to be mutually locally derivable from each other, if one tiling can be obtained from the other by a simple local rule (such as deleting or inserting an edge)

List

This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by expanding it with reliably sourced entries.
ImageNameNumber of tilesSpacePublication DateRefs.Comments
Trilobite and cross tiles2E21999[4]Tilings MLD from the chair tilings
Penrose P1 tiles6E21974[5][6]Tilings MLD from the tilings by P2 and P3, Robinson triangles, and "Starfish, ivy leaf, hex"
Penrose P2 tiles2E21977[7][8]Tilings MLD from the tilings by P1 and P3, Robinson triangles, and "Starfish, ivy leaf, hex"
Penrose P3 tiles2E21978[9][10]Tilings MLD from the tilings by P1 and P2, Robinson triangles, and "Starfish, ivy leaf, hex"
Binary tiles2E21988[11][12]Although similar in shape to the P3 tiles, the tilings are not MLD from each other. Developed in an attempt to model the atomic arrangement in binary alloys
Robinson tiles6E21971[13][14]Tiles enforce aperiodicity by forming an infinite hierarchy of square lattices
No imageAmmann A1 tiles6E21977[15][16]Tiles enforce aperiodicity by forming an infinite hierarchal binary tree.
Ammann A2 tiles2E21986[17][18]
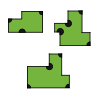Ammann A3 tiles3E21986[17][18]
Ammann A4 tiles2E21986[17][18][19]Tilings MLD with Ammann A5.
Ammann A5 tiles2E21982[20][21][22]Tilings MLD with Ammann A4.
No imagePenrose Hexagon-Triangle tiles2E21997[23][23][24]
No imageGolden Triangle tiles10E22001[25][26]date is for discovery of matching rules. Dual to Ammann A2
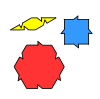Socolar tiles3E21989[27][28][29]Tilings MLD from the tilings by the Shield tiles
Shield tiles4E21988[30][31][32]Tilings MLD from the tilings by the Socolar tiles
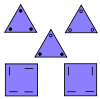Square triangle tiles5E21986[33][34]
Sphinx tiling91E2[35]
Starfish, ivy leaf and hex tiles3E2[36][37][38]Tiling is MLD to Penrose P1, P2, P3, and Robinson triangles
Robinson triangle4E2[17]Tiling is MLD to Penrose P1, P2, P3, and "Starfish, ivy leaf, hex".
Danzer triangles6E21996[39][40]
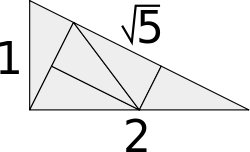Pinwheel tilesE21994[41][42][43][44]Date is for publication of matching rules.
Socolar–Taylor tile1E22010[45][46]Not a connected set. Aperiodic hierarchical tiling.
No imageWang tiles20426E21966[47]
No imageWang tiles104E22008[48]
No imageWang tiles52E21971[13][49]Tiles enforce aperiodicity by forming an infinite hierarchy of square lattices
Wang tiles32E21986[50]Locally derivable from the Penrose tiles.
No imageWang tiles24E21986[50]Locally derivable from the A2 tiling
Wang tiles16E21986[17][51]Derived from tiling A2 and its Ammann bars
Wang tiles14E21996[52][53]
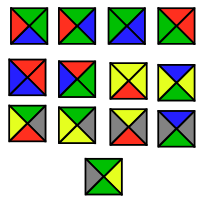Wang tiles13E21996[54][55]
No imageDecagonal Sponge tile1E22002[56][57]Porous tile consisting of non-overlapping point sets
No imageGoodman-Strauss strongly aperiodic tiles85H22005[58]
No imageGoodman-Strauss strongly aperiodic tiles26H22005[59]
Böröczky hyperbolic tile1Hn1974[60][61][59][62]Only weakly aperiodic
No imageSchmitt tile1E31988[63]Screw-periodic
Schmitt–Conway–Danzer tile1E3[63]Screw-periodic and convex
Socolar-Taylor tile1E32010[45][46]Periodic in third dimension
No imagePenrose rhombohedra2E31981[64][65][66][67][68][69][70][71]
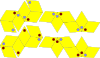Mackay-Amman rhombohedra4E31981[36]Icosahedral symmetry. These are decorated Penrose rhombohedra with a matching rule that force aperiodicity.
No imageWang cubes21E31996[72]
No imageWang cubes18E31999[73]
No imageDanzer tetrahedra4E31989[74][75]
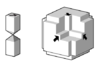I and L tiles2En for all n ≥ 31999[76]

References

  1. ↑ Grünbaum, Branko; Shephard, Geoffrey C. (1977), "Tilings by Regular Polygons", Math. Mag., 50 (5): 227–247, doi:10.2307/2689529, JSTOR 2689529
  2. ↑ Edwards, Steve, "Fundamental Regions and Primitive cells", Tiling Plane & Fancy, Kennesaw State University, archived from the original on 2010-09-16, retrieved 2017-01-11
  3. ↑ Wagon, Steve (2010), Mathematica in Action (3rd ed.), Springer Science & Business Media, p. 268, ISBN 9780387754772
  4. ↑ Goodman-Strauss, Chaim (1999), "A Small Aperiodic Set of Planar Tiles", European J. Combin., 20 (5): 375–384, doi:10.1006/eujc.1998.0281 (preprint available)
  5. ↑ Penrose, Roger (1974), "The role of Aesthetics in Pure and Applied Mathematical Research", Bull. Inst. Math. and its Appl., 10 (2): 266–271
  6. ↑ Mikhael, Jules (2010), Colloidal Monolayers On Quasiperiodic Laser Fields (PDF) (Dr. rer. nat thesis), p. 23, archived (PDF) from the original on 2010-09-28
  7. ↑ Gardner, Martin (January 1977), "Mathematical Games: Extraordinary nonperiodic tiling that enriches the theory of tiles", Scientific American, 236 (1): 110–121, Bibcode:1977SciAm.236a.110G, doi:10.1038/scientificamerican0177-110
  8. ↑ Gardner, Martin (1997), Penrose Tiles to Trapdoor Ciphers (Revised ed.), The Mathematical Association of America, p. 86, ISBN 9780883855218
  9. ↑ Penrose, Roger (1978), "Pentaplexity", Eureka, 39: 16–22
  10. ↑ Penrose, Roger (1979), "Pentaplexity", Math. Intell., 2 (1): 32–37, doi:10.1007/bf03024384, archived from the original on 2010-09-23
  11. ↑ Lançon, F.; Billard, L. (1988), "Two-dimensional system with a quasi-crystalline ground state" (PDF), Journal de Physique, 49 (2): 249–256, doi:10.1051/jphys:01988004902024900, archived (PDF) from the original on 2010-09-29
  12. ↑ Godrèche, C.; Lançon, F. (1992), "A simple example of a non-Pisot tiling with five-fold symmetry" (PDF), J. Phys. I France, 2 (2): 207–220, Bibcode:1992JPhy1...2..207G, doi:10.1051/jp1:1992134, archived (PDF) from the original on 2010-09-29
  13. 1 2 Robinson, Raphael M. (1971), "Undecidability and nonperiodicity of tilings in the plane", Inventiones Mathematicae, 12 (3): 177–209, Bibcode:1971InMat..12..177R, doi:10.1007/BF01418780
  14. ↑ Goodman-Strauss, Chaim (1999), Sadoc, J. F.; Rivier, N., eds., "Aperiodic Hierarchical tilings", NATO ASI Series, Series E: Applied Sciences, 354 (Foams and Emulsions): 481–496, doi:10.1007/978-94-015-9157-7_28, ISBN 978-90-481-5180-6
  15. ↑ Gardner, Martin (2001), The Colossal Book of Mathematics, W. W. Norton & Company, p. 76, ISBN 978-0393020236
  16. ↑ Grünbaum, Branko & Shephard, Geoffrey C. (1986), Tilings and Patterns, New York: W. H. Freeman, ISBN 0-7167-1194-X , according to Dutch, Steven (2003), Aperiodic Tilings, University of Wisconsin - Green Bay ; cf. Savard, John J. G., Aperiodic Tilings Within Conventional Lattices
  17. 1 2 3 4 5 Grünbaum, Branko & Shephard, Geoffrey C. (1986), Tilings and Patterns, New York: W. H. Freeman, ISBN 0-7167-1194-X
  18. 1 2 3 Ammann, Robert; Grünbaum, Branko; Shephard, Geoffrey C. (July 1992), "Aperiodic tiles", Discrete & Computational Geometry, 8 (1): 1–25, doi:10.1007/BF02293033
  19. ↑ Harriss, Edmund; Frettlöh, Dirk, "Ammann A4", Tilings Encyclopedia, Bielefeld University
  20. ↑ Beenker, F. P. M. (1982), Algebraic theory of non-periodic tilings of the plane by two simple building blocks: a square and a rhombus, TH Report, 82-WSK04, Eindhoven University of Technology
  21. ↑ Komatsu, Kazushi; Nomakuchi, Kentaro; Sakamoto, Kuniko; Tokitou, Takashi (2004), "Representation of Ammann-Beenker tilings by an automaton", Nihonkai Math. J., 15 (2): 109–118, archived from the original on 2010-09-29
  22. ↑ Harriss, Edmund; Frettlöh, Dirk, "Ammann-Beenker", Tilings Encyclopedia, Bielefeld University
  23. 1 2 Penrose, R. (1997), "Remarks on tiling: Details of a (1+ε+ε2) aperiodic set.", NATO ASI Series, Series C: Mathematical and Physical Sciences, 489 (The Mathematics of Long-Range Aperiodic Order): 467–497, doi:10.1007/978-94-015-8784-6_18, ISBN 978-0-7923-4506-0
  24. ↑ Goodman-Strauss, Chaim (2003), An aperiodic pair of tiles (PDF), University of Arkansas
  25. ↑ Danzer, Ludwig; van Ophuysen, Gerrit (2001), "A species of planar triangular tilings with inflation factor ", Res. Bull. Panjab Univ. Sci., 50 (1–4): 137–175, MR 1914493
  26. ↑ Gelbrich, G (1997), "Fractal Penrose tiles II. Tiles with fractal boundary as duals of Penrose triangles", Aequationes Mathematicae, 54: 108–116, doi:10.1007/bf02755450, MR 1466298
  27. ↑ Socolar, Joshua E. S. (1989), "Simple octagonal and dodecagonal quasicrystals", Physical Review B, 39 (15): 10519–51, Bibcode:1989PhRvB..3910519S, doi:10.1103/PhysRevB.39.10519
  28. ↑ Gähler, Franz; Lück, Reinhard; Ben-Abraham, Shelomo I.; Gummelt, Petra (2001), "Dodecagonal tilings as maximal cluster coverings", Ferroelectrics, 250 (1): 335–338, doi:10.1080/00150190108225095
  29. ↑ Savard, John J. G., The Socolar tiling
  30. ↑ Gähler, Franz (1988), "Crystallography of dodecagonal quasicrystals"" (PDF), in Janot, Christian, Quasicrystalline materials: Proceedings of the I.L.L. / Codest Workshop, Grenoble, 21–25 March 1988, Singapore: World Scientific, pp. 272–284
  31. ↑ Gähler, Franz; Frettlöh, Dirk, "Shield", Tilings Encyclopedia, Bielefeld University
  32. ↑ Gähler, Franz (1993), "Matching rules for quasicrystals: the composition-decomposition method" (PDF), Journal of Non-crystalline Solids, 153–154 (Proceddings of the Fourth International Conference on Quasicrystals): 160–164, Bibcode:1993JNCS..153..160G, doi:10.1016/0022-3093(93)90335-u, archived (PDF) from the original on 2010-10-01
  33. ↑ Stampfli, P. (1986), "A Dodecagonal Quasiperiodic Lattice in Two Dimensions", Helv. Phys. Acta, 59: 1260–1263
  34. ↑ Hermisson, Joachim; Richard, Christoph; Baake, Michael (1997), "A Guide to the Symmetry Structure of Quasiperiodic Tiling Classes", J. Phys. I France, 7 (8): 1003–1018, Bibcode:1997JPhy1...7.1003H, CiteSeerX 10.1.1.46.5796, doi:10.1051/jp1:1997200
  35. ↑ Goodman-Strauss, Chaim (2009), "Aperiodic Tilings" (PDF), Quasi periodic tile and language theory, Kyoto, 8–10 June, 2009, p. 74
  36. 1 2 Lord, Eric. A. (1991), "Quasicrystals and Penrose patterns" (PDF), Current Science, 61 (5): 313–319, archived (PDF) from the original on September 27, 2010
  37. ↑ Olamy, Z.; Kléman, M. (1989), "A two dimensional aperiodic dense tiling" (PDF), J. Phys. France, 50 (1): 19–33, doi:10.1051/jphys:0198900500101900, archived (PDF) from the original on 2010-11-01
  38. ↑ Mihalkovič, M.; Henley, C. L.; Widom, M. (2004), "Combined energy-diffraction data refinement of decagonal AlNiCo", Journal of Non-Crystalline Solids, 334–335 (8th International Conference on Quasicrystals): 177–183, arXiv:cond-mat/0311613, Bibcode:2004JNCS..334..177M, doi:10.1016/j.jnoncrysol.2003.11.034
  39. ↑ Nischke, K.-P.; Danzer, L. (1996), "A construction of inflation rules based on n-fold symmetry", Discrete & Computational Geometry, 15 (2): 221–236, doi:10.1007/bf02717732
  40. ↑ Hayashi, Hiroko; Kawachi, Yuu; Komatsu, Kazushi; Konda, Aya; Kurozoe, Miho; Nakano, Fumihiko; Odawara, Naomi; Onda, Rika; Sugio, Akinobu; Yamauchi, Masatetsu (2009), "Abstract: Notes on vertex atlas of planar Danzer tiling" (PDF), Japan Conference on Computational Geometry and Graphs, Kanazawa, November 11–13, 2009
  41. ↑ Radin, Charles (1994), "The pinwheel tilings of the plane", Annals of Mathematics, Second Series, 139 (3): 661–702, CiteSeerX 10.1.1.44.9723, doi:10.2307/2118575, JSTOR 2118575, MR 1283873, retrieved 2013-09-25
  42. ↑ Radin, Charles (1993), "Symmetry of Tilings of the Plane", Bull. Amer. Math. Soc., 29: 213–217, CiteSeerX 10.1.1.45.5319, doi:10.1090/s0273-0979-1993-00425-7
  43. ↑ Radin, Charles; Wolff, Mayhew (1992), "Space tilings and local isomorphism", Geom. Dedicata, 42 (3): 355–360, doi:10.1007/bf02414073, MR 1164542
  44. ↑ Radin, C (1997), "Aperiodic tilings, ergodic theory, and rotations", NATO ASI Series, Series C: Mathematical and Physical Sciences, Kluwer Acad. Publ., Dordrecht, 489 (The mathematics of long-range aperiodic order), MR 1460035
  45. 1 2 Socolar, Joshua E. S.; Taylor, Joan M. (2011), "An aperiodic hexagonal tile", Journal of Combinatorial Theory, Series A, 118 (8): 2207–2231, arXiv:1003.4279v1, doi:10.1016/j.jcta.2011.05.001
  46. 1 2 Socolar, Joshua E. S.; Taylor, Joan M. (2011), "Forcing nonperiodicity with a single tile", The Mathematical Intelligencer, 34 (1): 18–28, arXiv:1009.1419v1, doi:10.1007/s00283-011-9255-y
  47. ↑ Burger, Robert (1966), "The Undecidability of the Domino Problem", Memoirs of the American Mathematical Society, 66, doi:10.1090/memo/0066, ISBN 978-0-8218-1266-2
  48. ↑ Ollinger, Nicolas (2008), Two-by-two Substitution Systems and the Undecidability of the Domino Problem (PDF), Lecture Notes in Computer Science, 5028, Springer, pp. 476–485, doi:10.1007/978-3-540-69407-6_51
  49. ↑ Kari, J.; Papasoglu, P. (1999), "Deterministic Aperiodic Tile Sets", Geometric and Functional Analysis, 9 (2): 353–369, doi:10.1007/s000390050090
  50. 1 2 Lagae, Ares; Kari, Jarkko; Dutré, Phillip (2006), Aperiodic Sets of Square Tiles with Colored Corners, Report CW, 460, KU Leuven, p. 12, CiteSeerX 10.1.1.89.1294, archived from the original on 2010-10-02
  51. ↑ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw (2000), Pattern Formation in Biology, Vision and Dynamics, Singapore: World Scientific, ISBN 981-02-3792-8
  52. ↑ Kari, Jarkko (1996), "A small aperiodic set of Wang tiles", Discrete Mathematics, 160 (1–3): 259–264, doi:10.1016/0012-365X(95)00120-L
  53. ↑ Lagae, Ares (2007), Tile Based Methods in Computer Graphics (PDF) (PhD thesis), KU Leuven, p. 149, ISBN 978-90-5682-789-2, archived from the original (PDF) on 2010-10-06
  54. ↑ Culik, Karel; Kari, Jarkko (1997), On aperiodic sets of Wang tiles, Lecture Notes in Computer Science, 1337, pp. 153–162, doi:10.1007/BFb0052084
  55. ↑ Culik, Karel (1996), "An aperiodic set of 13 Wang tiles", Discrete Mathematics, 160 (1–3): 245–251, CiteSeerX 10.1.1.53.5421, doi:10.1016/S0012-365X(96)00118-5
  56. ↑ Zhu, Feng (2002), The Search for a Universal Tile (PDF) (BA thesis), Williams College
  57. ↑ Bailey, Duane A.; Zhu, Feng (2001), A Sponge-Like (Almost) Universal Tile (PDF), CiteSeerX 10.1.1.103.3739
  58. ↑ Goodman-Strauss, Chaim (2010), "A hierarchical strongly aperiodic set of tiles in the hyperbolic plane" (PDF), Theoretical Computer Science, 411 (7–9): 1085–1093, doi:10.1016/j.tcs.2009.11.018
  59. 1 2 Goodman-Strauss, Chaim (2005), "A strongly aperiodic set of tiles in the hyperbolic plane", Invent. Math., 159: 130–132, Bibcode:2004InMat.159..119G, doi:10.1007/s00222-004-0384-1
  60. ↑ Böröczky, K. (1974), "Gömbkitöltések állandó görbületü terekben I", Matematikai Lapok, 25: 265–306
  61. ↑ Böröczky, K. (1974), "Gömbkitöltések állandó görbületü terekben II", Matematikai Lapok, 26: 67–90
  62. ↑ Dolbilin, Nikkolai; Frettlöh, Dirk (2010), "Properties of Böröczky tilings in high dimensional hyperbolic spaces" (PDF), European J. Combin., 31 (4): 1181–1195, arXiv:0705.0291, doi:10.1016/j.ejc.2009.11.016
  63. 1 2 Radin, Charles (1995), "Aperiodic tilings in higher dimensions" (pdf), Proceedings of the American Mathematical Society, American Mathematical Society, 123 (11): 3543–3548, doi:10.2307/2161105, JSTOR 2161105, retrieved 2013-09-25
  64. ↑ Mackay, Alan L. (1981), "De Nive Quinquangula: On the pentagonal snowflake" (PDF), Sov. Phys. Crystallogr., 26 (5): 517–522, archived (PDF) from the original on 2010-10-06
  65. ↑ Meisterernst, Götz, Experimente zur Wachstumskinetik Dekagonaler Quasikristalle (PDF) (Dissertation), Ludwig Maximilian University of Munich, pp. 18–19, archived (PDF) from the original on 2010-10-08
  66. ↑ Jirong, Sun (1993), "Structure Transition of the Three-Dimensional Penrose Tiling Under Phason Strain Field", Chinese Phys. Lett., 10 (8): 449–452, Bibcode:1993ChPhL..10..449S, doi:10.1088/0256-307x/10/8/001
  67. ↑ Inchbald, Guy (2002), A 3-D Quasicrystal Structure
  68. ↑ Lord, E. A.; Ranganathan, S.; Kulkarni, U. D. (2001), "Quasicrystals: tiling versus clustering" (PDF), Philosophical Magazine A, 81 (11): 2645–2651, doi:10.1080/01418610108216660, archived (PDF) from the original on 2010-10-06
  69. ↑ Rudhart, Christoph Paul (June 1999), Zur numerischen Simulation des Bruchs von Quasikristallen (Thesis), University of Stuttgart, p. 11, doi:10.18419/opus-4639
  70. ↑ Lord, E. A.; Ranganathan, S.; Kulkarni, U. D. (2000), "Tilings, coverings, clusters and quasicrystals" (PDF), Current Science, 78 (1): 64–72, archived (PDF) from the original on 2010-11-01
  71. ↑ Katz, A. (1988), "Theory of Matching Rules for the 3-Dimensional Penrose Tilings", Communications in Mathematical Physics, 118 (2): 263–288, Bibcode:1988CMaPh.118..263K, doi:10.1007/BF01218580
  72. ↑ Culik, Karel; Kari, Jarkko (1995), "An aperiodic set of Wang cubes", The Journal of Universal Computer Science, 1 (10), CiteSeerX 10.1.1.54.5897, doi:10.3217/jucs-001-10-0675
  73. ↑ Walther. Gerd; Selter, Christoph, eds. (1999), Mathematikdidaktik als design science : Festschrift für Erich Christian Wittmann, Leipzig: Ernst Klett Grundschulverlag, ISBN 3-12-200060-1
  74. ↑ Danzer, L. (1989), "Three-Dimensional Analogs of the Planar Penrose Tilings and Quasicrystals", Discrete Mathematics, 76 (1): 1–7, doi:10.1016/0012-365X(89)90282-3
  75. ↑ Zerhusen, Aaron (1997), Danzer's three dimensional tiling, University of Kentucky
  76. ↑ Goodman-Strauss, Chaim (1999), "An Aperiodic Pair of Tiles in En for all n ≥ 3", European J. Combin., 20 (5): 385–395, doi:10.1006/eujc.1998.0282 (preprint available)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.