Traced monoidal category
In category theory, a traced monoidal category is a category with some extra structure which gives a reasonable notion of feedback.
A traced symmetric monoidal category is a symmetric monoidal category C together with a family of functions
called a trace, satisfying the following conditions (where we sometimes denote an identity morphism by the corresponding object, e.g., using U to denote ):
- naturality in X: for every and ,
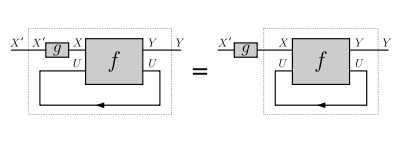
Naturality in X
- naturality in Y: for every and ,
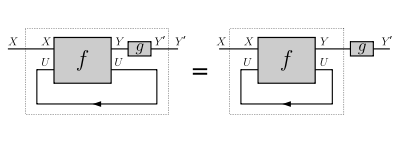
Naturality in Y
- dinaturality in U: for every and
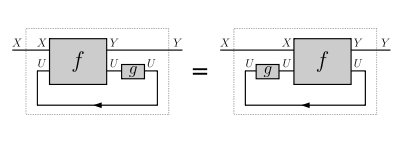
Dinaturality in U
- vanishing I: for every ,
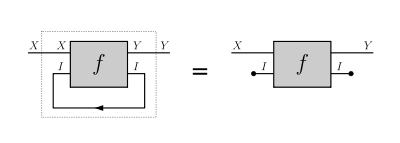
Vanishing I
- vanishing II: for every
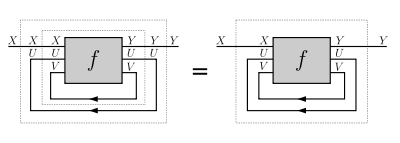
Vanishing II
- superposing: for every and ,
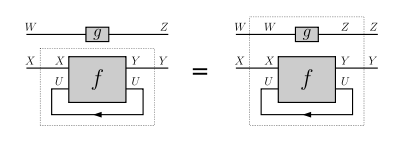
Superposing
- yanking:
(where is the symmetry of the monoidal category).
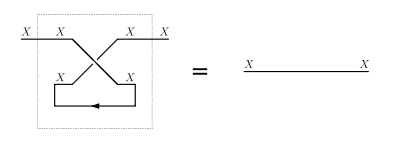
Yanking
Properties
- Every compact closed category admits a trace.
- Given a traced monoidal category C, the Int construction generates the free (in some bicategorical sense) compact closure Int(C) of C.
References
- André Joyal, Ross Street, Dominic Verity (1996). "Traced monoidal categories". Mathematical Proceedings of the Cambridge Philosophical Society. 3: 447–468. doi:10.1017/S0305004100074338.
This article is issued from
Wikipedia.
The text is licensed under Creative Commons - Attribution - Sharealike.
Additional terms may apply for the media files.