Planar straight-line graph

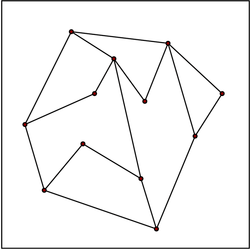
An example of planar straight-line graph

In computational geometry, a planar straight-line graph, in short PSLG, (or straight-line plane graph, or plane straight-line graph) is a term used for an embedding of a planar graph in the plane such that its edges are mapped into straight line segments.[1] Fáry's theorem (1948) states that every planar graph has this kind of embedding.

In computational geometry, PSLGs have often been called planar subdivisions, with an assumption or assertion that subdivisions are polygonal.

A PSLG without vertices of degree 1 defines a subdivision of the plane into polygonal regions and vice versa. The absence of vertices of degree 1 simplifies descriptions of various algorithms, but it is not essential.

PSLGs may serve as representations of various maps, e.g., geographical maps in geographical information systems.

Special cases of PSLGs are triangulations (polygon triangulation, point set triangulation). Point set triangulations are maximal PSLGs in the sense that it is impossible to add straight edges to them while keeping the graph planar. Triangulations have numerous applications in various areas.

PSLGs may be seen as a special kind of Euclidean graphs. However, in discussions involving Euclidean graphs, the primary interest is their metric properties, i.e., distances between vertices, while for PSLGs the primary interest is the topological properties. For some graphs, such as Delaunay triangulations, both metric and topological properties are of importance.

Problems in terms of PSLG

  • Point location. For a query point, find which face of the PSLG it belongs to.
  • Map overlay. Find the overlay of two PSLGs (maps), which is the subdivision of the plane by the two simultaneously embedded PSLGs. In GIS this problem is known as "thematic map overlay".

See also

References

  1. ↑ Franco P. Preparata and Michael Ian Shamos (1985). Computational Geometry - An Introduction. Springer-Verlag. 1st edition: ISBN 0-387-96131-3; 2nd printing, corrected and expanded, 1988: ISBN 3-540-96131-3; Russian translation, 1989: ISBN 5-03-001041-6.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.