Dual object

In category theory, a branch of mathematics, a dual object is an analogue of a dual vector space from linear algebra for objects in arbitrary monoidal categories. It's only a partial generalization, based upon the categorical properties of duality for finite-dimensional vector spaces. An object admitting a dual is called a dualizable object. In this formalism, infinite-dimensional vector spaces are not dualizable, since the dual vector space V^∗ doesn't satisfy the axioms.^[1] Often, an object is dualizable only when it satisfies some finiteness or compactness property.^[2]

A category in which each object has a dual is called autonomous or rigid. A category of finite-dimensional vector spaces with a standard tensor product is rigid, while the category of all vector spaces is not.

Motivation

Let V be a finite-dimensional vector space over some field k. A standard notion of a dual vector space V^∗ has the following property. For any vector spaces U and W there is an adjunction Hom_k(U ⊗ V,W) = Hom_k(U, V^∗ ⊗ W), and this characterizes V^∗ up to a unique isomorphism. This expression makes sense in any category with an appropriate replacement for the tensor product of vector spaces. For any monoidal category (C, ⊗) one may attempt to define a dual of an object V to be an object V^∗ ∈ C with a natural isomorphism of bifunctors

Hom_C((–)₁ ⊗ V, (–)₂) → Hom_C((–)₁, V^∗ ⊗ (–)₂)

For a well-behaved notion of duality, this map should be not only natural in the sense of category theory, but also respect the monoidal structure in some way.^[1] An actual definition of a dual object is thus more complicated.

In a closed monoidal category C, i.e. a monoidal category with an internal Hom functor, an alternative approach is to simulate the standard definition of a dual vector space as a space of functionals. For an object V ∈ C define V^∗ to be ${\underline {\mathrm {Hom} }}_{C}(V,\mathbb {1} _{C})$ , where 1_C is the monoidal identity. In some cases, this object will be a dual object to V in a sense above, but in general it leads to a different theory.^[3]

Definition

Consider an object $X$ in a monoidal category $({\mathbf {C}},\otimes ,I,\alpha ,\lambda ,\rho )$ . The object $X^{*}$ is called a left dual of $X$ if there exist two morphsims

\eta :I\to X\otimes X^{*}

, called the coevaluation, and

\varepsilon :X^{*}\otimes X\to I

, called the evaluation,

such that the following two diagrams commute

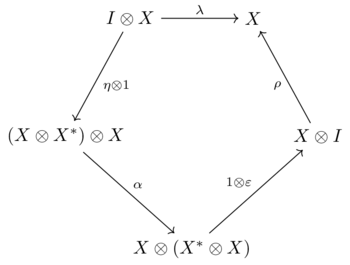and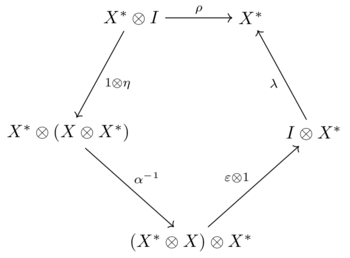

The object $X$ is called the right dual of $X^{*}$ . Left duals are canonically isomorphic when they exist, as are right duals. When C is braided (or symmetric), every left dual is also a right dual, and vice versa.

If we consider a monoidal category as a bicategory with one object, a dual pair is exactly an adjoint pair.

Examples

Consider a monoidal category (Vect_k, ⊗_k) of vector spaces over a field k with a standard tensor product. A space V is dualizable if and only if it's a finite-dimensional vector space. In that case the dual object V^∗ coincides with the standard notion of a dual vector space.
Consider a monoidal category (Mod_R, ⊗_R) of modules over a ring R with a standard tensor product. A module M is dualizable if and only if it's a finitely generated projective module. In that case the dual object R^∗ is also given by the module of homomorphisms Hom_R(M, R).
Consider a homotopy category of pointed spectra Ho(Sp) with a smash product as a monoidal structure. If M is a compact neighborhood retract in $\mathbb {R} ^{n}$ (for example, a compact smooth manifold), then the corresponding pointed spectrum Σ^∞(M⁺) is dualizable. This is a consequence of Spanier–Whitehead duality, which implies in particular Poincaré duality for compact manifolds.^[1]
The category $\mathrm {End} (\mathbf {C} )$ of endofunctors of $\mathbf {C}$ is a monoidal category under functor composition. It is true that a functor $F$ is a left dual of a functor $G$ iff $F\dashv G$ , that is if $F$ is left adjoint to $G$ .^[4]

Categories with duals

A monoidal category where every object has a left (respectively right) dual is sometimes called a left (respectively right) autonomous category. Algebraic geometers call it a left (respectively right) rigid category. A monoidal category where every object has both a left and a right dual is called an autonomous category. An autonomous category that is also symmetric is called a compact closed category.

References

1 2 3 Ponto, Kate; Shulman, Michael (2014). "Traces in symmetric monoidal categories". Expositiones Mathematicae. 32 (3): 248–273. arXiv:1107.6032. Bibcode:2011arXiv1107.6032P.
↑ Becker, James C.; Gottlieb, Daniel Henry (1999). "A history of duality in algebraic topology" (PDF). In James, I.M. History of topology. North Holland. pp. 725–745. ISBN 9780444823755.
↑ "dual object in a closed category in nLab". ncatlab.org. Retrieved 11 December 2017.
↑ See for example exercise 2.10.4 in Pavel Etingof "Tensor Categories"

Peter Freyd and David Yetter (1989). "Braided Compact Closed Categories with Applications to Low-Dimensional Topology". Advances in Mathematics. 77 (2): 156–182. doi:10.1016/0001-8708(89)90018-2.
André Joyal and Ross Street. "The Geometry of Tensor calculus II". Synthese Lib. 259: 29–68.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[traces-1] 1 2 3 Ponto, Kate; Shulman, Michael (2014). "Traces in symmetric monoidal categories". Expositiones Mathematicae. 32 (3): 248–273. arXiv:1107.6032. Bibcode:2011arXiv1107.6032P.

[2] Becker, James C.; Gottlieb, Daniel Henry (1999). "A history of duality in algebraic topology" (PDF). In James, I.M. History of topology. North Holland. pp. 725–745. ISBN 9780444823755.

[3] "dual object in a closed category in nLab". ncatlab.org. Retrieved 11 December 2017.

[4] See for example exercise 2.10.4 in Pavel Etingof "Tensor Categories"