Problem 2
|
Compute
|
Solution 2
We will compute the general case:
Find Poles of f(z)
The poles of are just the zeros of , so we can compute them in the following manner:
If is a solution of ,
then
and
, k=0,1,2,...,n-1.
Thus, the poles of are of the form with
Choose Path of Contour Integral
In order to get obtain the integral of from 0 to , let us consider the path consisting in a line going from 0 to , then the arc of radius from the angle 0 to and then the line joining the end point of and the initial point of ,
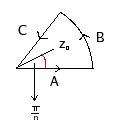
where is a fixed positive number such that
the pole is inside the curve . Then , we need to estimate the integral
Compute Residues of f at z0= exp{i\pi /n}
Bound Arc Portion (B) of Integral
Hence as ,
Parametrize (C) in terms of (A)
Let where is real number. Then
Apply Cauchy Integral Formula
From Cauchy Integral Formula, we have,
As , . Also can be written in terms of . Hence
We then have,
Problem 4
|
Suppose and there is an entire function with . If and , prove that |
Solution 4
Lemma: Two fixed points imply identity
Lemma. Let be analytic on the unit , and assume that on the disc. Prove that if there exist two distinct points and in the disc which are fixed points, that is, and , then .
Proof Let be the automorphism defined as
Consider now . Then, F has two fixed points, namely
.
Since ,
(since is different to ), and
,
by Schwarz Lemma,
.
But, replacing into the last formula, we get .
Therefore,
,
which implies
Shift Points to Create Fixed Points
Let . Then and .
Notice that is an infinite horizontal strip centered around the real axis with height . Since is a unit horizontal shift left, .
Use Riemann Mapping Theorem
From the Riemann mapping theorem, there exists a biholomorphic (bijective and holomorphic) mapping , from the open unit disk to .
Define Composition Function
Let . Then maps to .
From the lemma, since has two fixed points, which implies which implies .
Problem 6
|
Let be the family of functions analytic on so that
|
Solution 6
Choose any compact set K in D
Choose any compact set in the open unit disk . Since is compact, it is also closed and bounded.
We want to show that for all and all , is bounded i.e.
where is some constant dependent on the choice of .
Apply Maximum Modulus Principle to find |f(z0)|
Choose that is the shortest distance from the boundary of the unit disk . From the maximum modulus principle, .
Note that is independent of the choice of .
Apply Cauchy's Integral Formula to f^2(z0)
We will apply Cauchy's Integral formula to (instead of ) to take advantage of the hypothesis.
Choose sufficiently small so that
Integrate with respect to r
Integrating the left hand side, we have
Hence,
Bound |f(z0)| by using hypothesis
Apply Montel's Theorem
Then, since any is uniformly bounded in every compact set, by Montel's Theorem, it follows that is normal